01. Probability Review
Review Probability
Before Sebastian teaches you about localizing a robot, in the next couple concepts, we'll review how to represent uncertainty in robot motion and sensors. The next couple sections will include multiple videos and quizzes to check your understanding of probability and probability distributions. These are meant to prepare you for this lesson, so make sure to read this material carefully to become familiar with terminology and mathematical representations of uncertainty!
Probability Review
Before learning more about uncertainty in robot localization, let's review how to mathematically represent uncertainty using probability!
A classic example of an event with some certainty associated with it is a coin flip. A typical coin has two sides: heads and tails. Without me telling you anything else, what chance do you think a coin like this has of flipping and landing heads up?

Heads and tails of a coin.
SOLUTION:
P(H) = 0.5SOLUTION:
YesFormal Definition of Probability
The probability of an event, X, occurring is P(X). The value of P(X) must fall in a range of 0 to 1.
0 <= P(X) <= 1
An event, X, can have multiple outcomes which we might call X1, X2, .. and so on; the probabilities for all outcomes of X must add up to one. For example, say there are two possible outcomes, X1 and X2:
- If
P(X1) = 0.2thenP(X2) = 0.8because all possible outcomes must sum to 1.
Terminology
Independent Events
Events like coin flips are known as independent events; this means that the probability of a single flip does not affect the probability of another flip; P(H) will be 0.5 for each fair coin flip. When flipping a coin multiple times, each flip is an independent event because one flip does not affect the probability that another flip will land heads up or tails up.
Dependent Events
When two events are said to be dependent, the probability of one event occurring influences the likelihood of the other event. For example, say you are more likely to go outside if it's sunny weather. If the probability of sunny weather is low on a given day, the probability of you going outside will decrease as well, so the probability of going outside is dependent on the probability of sunny weather.
Joint Probability
The probability that two or more independent events will occur together (in the same time frame) is called a joint probability, and it is calculated by multiplying the probabilities of each independent event together. For example, the probability that you will flip a coin and it will lands heads up two times in a row can be calculated as follows:
- The probability of a coin flipping heads up,
P(H) = 0.5 - The joint probability of two events (a coin landing heads up) happening in a row, is the probability of the first event times the probability of the second event:
P(H)*P(H) = (0.5)*(0.5) = 0.25
Quantifying Certainty (and Uncertainty)
When we talk about being certain that a robot is at a certain location (x, y), moving a certain direction, or sensing a certain environment, we can quantify that certainty using probabilistic quantities. Sensor measurements and movement all have some uncertainty associated with them (ex. a speedometer that reads 50mph may be off by a few mph, depending on whether a car is moving up or down hill).
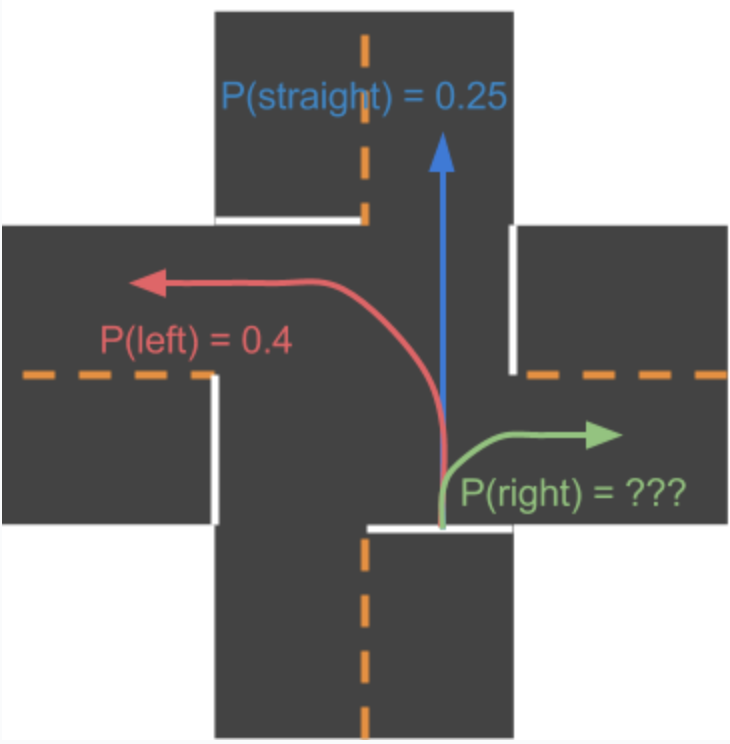
QUESTION:
At a particular intersection, cars can either:
Turn left
Go straight
Turn right
Cars tend to turn left with a probability of 0.4 and go straight with a probability of 0.25. What is the probability that a car turns right?
SOLUTION:
NOTE: The solutions are expressed in RegEx pattern. Udacity uses these patterns to check the given answer